Answer:
a = (4, 4)T is oriented at 45°
a = (4, 4)T is oriented at 45°
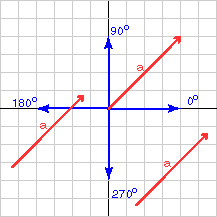
Math should give the same answer: The slope of a is
(change in y)/(change in x) = 4.0/4.0 = 1.0.
So the angle is arc tan( 1.0 ) = 45°.
Vectors have no location, so neither the length nor the direction depend on where you draw a vector. The formula for the direction of a 2D vector is
angle of (x, y)T = arc tan( y/x )
Arc tan( z ) means "find the angle that has a tangent of z." When you do this with a calculator, remember that the answer may be in radians or in degrees. Most calculators give you the option of using use either format.
Also, since calculators usually give the answer as -90.0 to +90.0 degrees (or -pi to +pi radians) you may have to adjust the answer. More on this later.
You can use the calculator on your computer.
If you are using MS Windows, click "scientific" in the "view" menu for
a calculator that has arc tan.
Arc tan may be labeled tan-1.
What is the orientation of the vector represented by: k = (3,4)T ? (Do this with a calculator.)