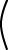Answer:


cos(w)     1 
    0  sin(w)


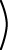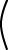x    2 
1    y


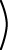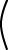x⋅cos(w)+1   2⋅cos(w) + y
  sin(w)   y⋅sin(w)

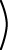Although most of our examples have used integers, don't forget that matrix elements can be real numbers or variables.

Summary of Rules (so far)

Here is a list of rules that this chapter has discussed. Each rule assumes that the matrices can be multiplied (their dimensions match correctly). Click on a rule to review the page that discusses it.

matrix product, dimensions when product can be formed

if A_M×K B_K×N = C, then C = C_M×N

matrix-matrix product, non-commutative Not Commutative:

AB =/= BA, except rarely.

matrix-matrix product, associative Associative:

A(BC) = (AB)C = ABC

matrix-matrix product, scalar factor Scalar factor:

a(AB) = (aA)B = aAB = A(aB)

matrix-matrix product, distributive Distributive:

A( B + C) = AB + AC

matrix-matrix product, distributive Distributive:

(A + B)C = AC + BC

matrix-matrix product, zero matrix Multiplication by zero:

0A = 0, for the zero matrix 0

You have reached the end of this chapter. The next chapter will discuss further properties of matrix-matrix multiplication.