Answer:
p = A-1 q
| p | = | 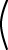 |
1 -2 0 1 |
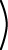 |
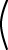 |
5 2 |
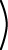 |
= | 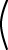 |
1 2 |
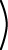 |
p = A-1 q
| p | = | 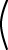 |
1 -2 0 1 |
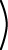 |
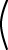 |
5 2 |
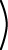 |
= | 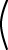 |
1 2 |
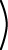 |
This is (hopefully) the same answer you got for p by trial and error a few pages ago.
If A is non-singular (has an inverse) and Ap = q, then p = A-1q.
The inverse of a non-singular square matrix is unique. One way to see this is that there is only one column matrix p that is the solution to Ap = q, so there must be only one A-1.
It might look like computing A-1 is a useful thing to do. In fact, A-1 is useful in discussions about matrices and transformations but not very useful for actual computation. Almost never do you really want to compute a matrix inverse.
For example, say that a column matrix p represents a point in a computer graphic world. If the viewpoint changes, the column matrix is transformed to q = Ap. You might talk about reversing the transformation by using A-1q. But almost always there is an easier way to return to the original viewpoint than computing an inverse.
What is (AB) (B-1 A-1) ?