Example
The vector w is represented by (6, 5)T.
The vector v is represented by (9, 0)T.
Find the projection of w onto v.
(Find kv and u.)
In the diagram the answer can simply be read off the
graph paper.
But pretend you didn't notice that.
- Compute the lengths:
- | w | =
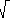 ((6, 5)T·(6, 5)T) = 7.81
((6, 5)T·(6, 5)T) = 7.81
- | v | =
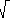 ((9, 0)T·(9, 0)T) = 9
((9, 0)T·(9, 0)T) = 9
- Compute the unit vectors:
- wu = (6, 5)T / 7.81
- vu = (9, 0)T / 9 = (1, 0)T
- Compute the cosine of the angle between the vectors:
- wu · vu
= (1/7.81) (6, 5)T · (1, 0)T
= 6/7.81
- Assemble the projection:
- kv = | w | (wu·vu) vu
- kv = 7.81 (6/7.81) (1, 0)T
= 6(1, 0)T = (6, 0)T
- Compute the orthogonal vector:
- u = w - kv
- u = (6, 5)T - (6, 0)T = (0, 5)T
The result is that w = (6, 0)T + (0, 5)T,
as expected.
Of course, the example was easy.

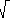 ((6, 5)T·(6, 5)T) = 7.81
((6, 5)T·(6, 5)T) = 7.81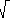 ((9, 0)T·(9, 0)T) = 9
((9, 0)T·(9, 0)T) = 9