Change the elements of this column matrix: (3, 4)T
so that the vector it represents
is twice as long and remains pointing in the same direction.
Answer:
You could carefully work out the correct answer using what you
already know.
Or you could take a guess and see if it works:
2 × (3, 4)T = (6, 8)T
Scaling
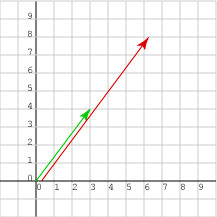
Does the guess work?
- (new length)2 = 62 + 82 =
22 32 + 22 42 =
22 (32+42) =
22 × (old length)2
- So, taking roots, (new length) = 2 × (old length)
- By similar triangles, the direction is the same.
Or you could notice: new direction = arc tan( 8/6 ) = arc tan( 4/3 ) = old direction.
It looks like the guess worked.
When talking about vectors,
a real number is sometimes called a scalar.
Scaling a geometrical vector means keeping its orientation
the same but changing its length by a scale factor.
It is like changing the scale of a picture;
the objects expand or shrink,
but the directions remain the same.
If a vector is represented by a column matrix (x, y)T
then scaling by the a number multiplies each element:
a(x, y)T = (ax, ay)T
This works for 3 dimensional vectors also:
If v is represented by (x, y, z)T then
av is represented by (ax, ay, az)T.
