a = ( 3, 2 )T b = (-2, 1 )T
Answer:
a + b = ( 1, 3 )T
a = ( 3, 2 )T b = (-2, 1 )T
a + b = ( 1, 3 )T
Vectors are geometric objects. A particular vector can be represented in a variety of ways. It is important to understand the difference between a geometric object (such as a point or a vector) and the way it is represented (often with a column matrix).
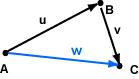
The diagram shows points A, B, and C (in two dimensions). A displacement is a distance and a direction. Vector u is the displacement from A to B. Vector v is the displacement from B to C.
The displacement from A to C is the vector w. The effect of moving through the displacement u and then through the displacement v is the same as moving through the displacement w. In symbols:
u + v = w
Does the addition depend on where the vectors are?