Theta
(skip if you want)

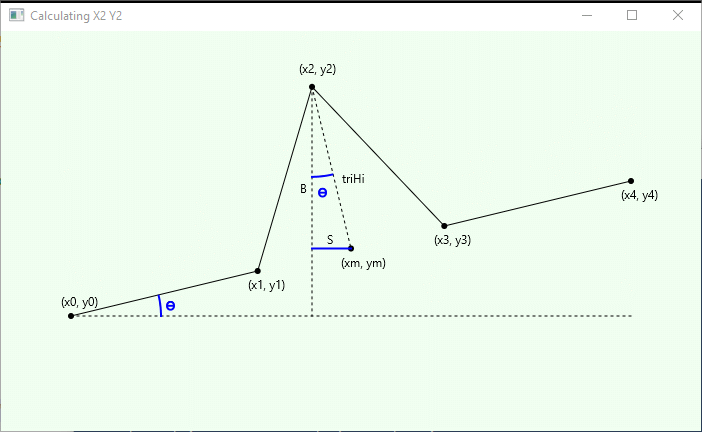
If you know the height of the triangle, triHi, the middle of the base, (xm, ym), and Θ you can figure out (x2, y2)

There are two angles Θ in the diagram. They are the same because the two lines that form the top angle are perpendicular to the two lines that form the bottom angle.

The tangent of Θ is the opposite side over the adjacent side. In the diagram, this is (y0-y4) over (x4-x0). (Remember that Y increases downward.) To get Θ calculate the arc tangent.

So theta = Math.atan2( (y0-y4),(x4-x0) ) ;

The function Math.atan2(Y,X) uses the signs of Y and X to put the angle in the correct quadrant. So (for example) if Y and X are both negative, the angle is in the third quadrant. The angle is in radians, and so is suitable for use with other trigonometric functions.