a(u•v) =  a|u||v| cosθ

 =  |au||v| cosθ

 =  (au)•v

 =  u•(av)

Cosine of 90°

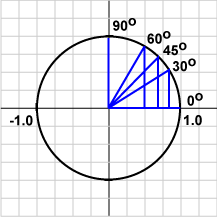
You may be somewhat fuzzy about how the cosine function behaves. Rather than memorize abstract stuff, visualize the unit circle with its radius projected onto the x-axis. From the picture,

the cosine of 0°   =   1.0,
the cosine of 30°   =   0.866,
the cosine of 45°   =   0.707,
the cosine of 60°   =   0.500,
the cosine of 90°   =   0.0.

Recall that:

u • v = |u| |v| cos θ