What is the cosine of the angle between the two unit vectors represented by (0.7071, 0.7071)T and (0.5, 0.866)T ?
Answer:
cos θ = (0.7071, 0.7071)T · (0.5, 0.866)T = 0.7071 · 0.5 + 0.7071 · 0.866 = 0.9659
What is the cosine of the angle between the two unit vectors represented by (0.7071, 0.7071)T and (0.5, 0.866)T ?
cos θ = (0.7071, 0.7071)T · (0.5, 0.866)T = 0.7071 · 0.5 + 0.7071 · 0.866 = 0.9659
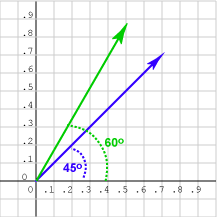
The first vector, (0.7071, 0.7071)T is a unit vector at 45°. The second vector, (0.5, 0.866)T is a unit vector at 60°. So the dot product should be the cosine of 15°, which it is. Another way to see this is with symbols.
Step 5 uses:
cos(x+y) = cos(x) cos(y) - sin(x) sin(y)
sin(x+y) = sin(x) cos(y) + cos(x) sin(y)
Step 9 uses:
sin2x + cos2x = 1
What is the cosine of the angle between the two unit vectors represented by qu = (0.0, 1)T and ru = (0.5, 0.866)T ?