Answer:
Yes. The result is the total displacement that would result in following each vector in turn.
Yes. The result is the total displacement that would result in following each vector in turn.
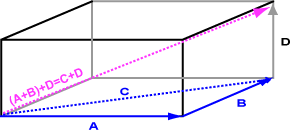
The above diagram shows the result of adding (a + b) + d = c + d. The result is the vector with length and direction the same as the diagonal of the figure.
The bottom diagram shows the result of adding a + (b + d). The result is the same. This is a demonstration of the associative property of vector addition:
a + (b + c) = (a + b) + c
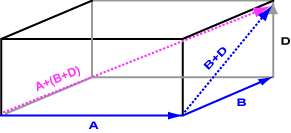
The rule works in all dimensions. Mostly the geometric vectors of computer graphics are two dimensional and three dimensional (although, in general, higher dimensions are possible).
The associative property means that sums of several vectors can be written like a + b + c + d + e without parentheses.
Say that you walk five blocks north, and then three blocks east.
If, instead, you had walked three blocks east and then five blocks north would you arrive at the same place?