x = ( x1, x2 ) y = ( 3.2, -8.6 ) x = y
Answer:
x1 = 3.2, and x2 = -8.6
x = ( x1, x2 ) y = ( 3.2, -8.6 ) x = y
x1 = 3.2, and x2 = -8.6
Column matrices are used to represent vectors and also used to represent points. In two dimensions, the same data type (two dimensional column matrices) is used to represent two different types of geometrical objects (points and vectors). This is awkward. Later on, this situation will be corrected.
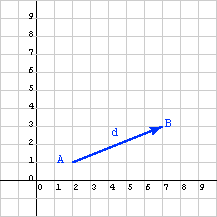
The figure shows a displacement vector representing the difference between two points in the x-y plane. (For now, the examples are in two dimensional space; three dimensional space will come later).
Computing the displacement from A to B can be done as two separate problems:
The displacement vector expressed as a matrix is:
d = (5, 2)T
Displacement vectors are often visualized as an arrow connecting two points. In the diagram point A is the tail of the vector and point B is the tip of the vector. (However, recall that vectors do not have a position, so this is just a convenient place to draw it, not where it is.)
The column matrix d represents the displacement vector from point A to point B. What column matrix represents displacement from point B to point A?