2N, twice the original integer.
0110 0001 = 9710.
1100 0010 = 19410.
(However, for unsigned binary, if a 1-bit is shifted off the left side, then the number is ruined).
sll d,s,shft # $d gets the bits in $s
# shifted left logical
# by shft positions,
# where 0 ≤ shft < 32
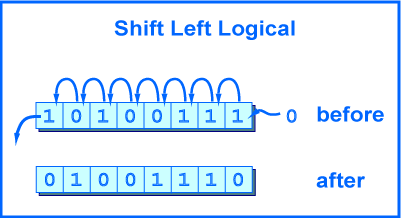
A shift left logical of one position moves each bit to the left by one. The low-order bit (the right-most bit) is replaced by a zero bit and the high-order bit (the left-most bit) is discarded.
Each bit in the original is shifted into the position to its left, which (for unsigned binary) corresponds to the next higher power of two. So if the original bits are regarded as unsigned binary, the bit in position N corresponds to 2N. A left shift moves the bit into the position for 2N+1. This happens for every bit, so the new pattern represents twice the original integer.
Shifting by two positions is the same as performing a one-position shift two times. Shifting by zero positions leaves the pattern unchanged. Shifting an N-bit pattern left by N or more positions changes all of the bits to zero.
The picture shows the operation performed on eight bits.
The original pattern is
1010 0111.
The resulting pattern is
0100 1110.
The MIPS processor always performs the operation on a 32-bit register and puts the result in a 32-bit register.
The ALU (arithmetic/logic unit) which does the operation pays no attention to what the bits mean. If the bits represent an unsigned integer, then a left shift is equivalent to multiplying the integer by two.