What do you suppose happens when the vectors are in opposite directions, such as (1, 0)T and (-1, 0)T ?
Answer:
The magnitude of the dot product is negative.
What do you suppose happens when the vectors are in opposite directions, such as (1, 0)T and (-1, 0)T ?
The magnitude of the dot product is negative.
Here is a sampling of bu and the dot product with au = (1.0, 0)T for various angles.
| Angle | b | Result | Picture |
|---|---|---|---|
| 000° | (1.000, 0.000)T | 1.000 | 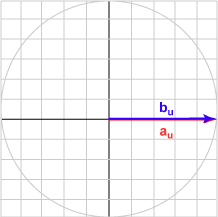 |
| 015° | (0.966, 0.259)T | 0.966 | 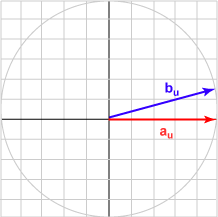 |
| 030° | (0.866, 0.500)T | 0.866 | 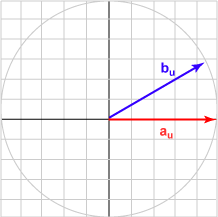 |
| 045° | (0.707, 0.707)T | 0.707 | 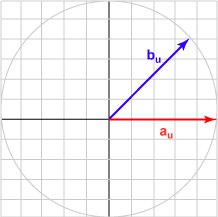 |
| 060° | (0.500, 0.866)T | 0.500 | 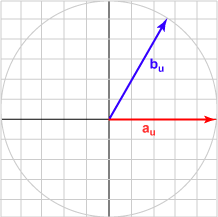 |
| 075° | (0.259, 0.966)T | 0.259 | 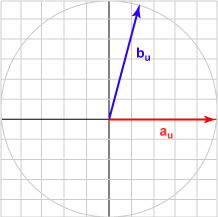 |
| 090° | (0.000, 1.000)T | 0.000 | 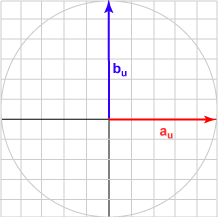 |
| 105° | (-0.500, 0.866)T | -0.259 | 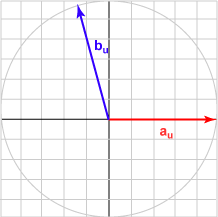 |
| 120° | (-0.500, 0.866)T | -0.500 | 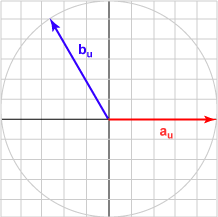 |
| 135° | (-0.707, 0.707)T | -0.707 | 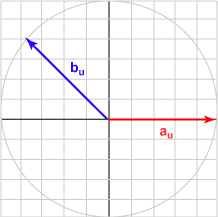 |
| 150° | (-0.866, 0.500)T | -0.866 | 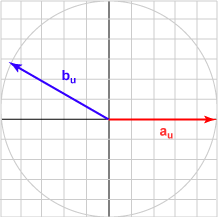 |
| 165° | (-0.966, 0.259)T | -0.966 | 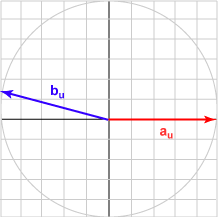 |
| 180° | (-1.000, 0.000)T | -1.000 | 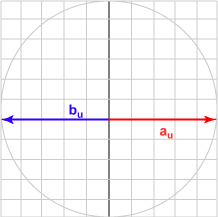 |
The bu in each case is the unit vector represented by (cos θ, sin θ )T .
What do you imagine is the range of values for the dot product of the two unit vectors, au · bu ?