Is it always true that AB = BA?
Answer:
NO! Even when both products can be formed they are rarely equal.
Is it always true that AB = BA?
NO! Even when both products can be formed they are rarely equal.
For example, calculate both of the following products (you might wish to use paper and pencil):
| Problem | Think First | Result |
|---|---|---|
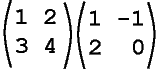 |
 | |
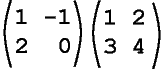 |
 |
This shows that in general for matrices A and B, AB ≠ BA.
Is A4×4 04×4 = 04×4 A4×4, where 0 is the zero matrtix?