If the product An×m Bm×p can be formed, will it always be possible to form the product Bm×p An×m?
Answer:
No. If n ≠ p then BA can't be formed. Later you will see that even if both products can be formed, it is rare that AB = BA.
If the product An×m Bm×p can be formed, will it always be possible to form the product Bm×p An×m?
No. If n ≠ p then BA can't be formed. Later you will see that even if both products can be formed, it is rare that AB = BA.
The matrix-matrix product AB is calculated by forming the dot product of each row of A with each column of B. Of course, the number of columns in A equal to the number of rows in B.
As in the previous chapter, flip a column of B so that its elements align with the rows of A. Form the dot product, which becomes row 1 col 1 of the result. Now slide down one row to form the next dot product, which becomes row 2 col 1 of the result. Continue down until the last row.
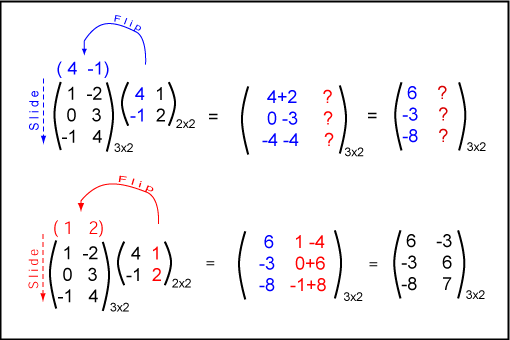
When you are finished with first column of B, move on to its next column and do the same thing. Continue with each column of B until all elements are calculated.
Note: Element ij of the result = dot product of row i of A with column j of B.
Say that you are forming the product A 5×3 B 3×2 = C 5×2
What row and column are used to calculate the 3rd row 2nd column of C ?