Another Example

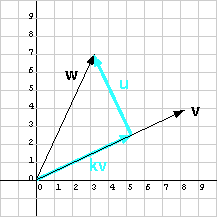
You don't have to compute the length of w. It cancels out before the final answer. And, all you need is the square of the length of v, |v|². Some books show formulae for projection that make use of these facts (but, to my taste, are less intuitive).

Here is another example, this time not so easy. The vector w is represented by by (3.2, 7)^T. The vector v is represented by by (8, 4)^T. Find kv and u.

1. Compute the lengths:

   | w |  =   (keep it symbolic)

   | v |²  =   (8, 4)^T·(8, 4)^T   =   80

2. Compute the unit vectors:

   w_u  =   (3.2, 7)^T / | w |

   v_u  =   (8, 4)^T / | v |

3. Compute the cosine of the angle between the vectors:

   w_u · v_u  =   (3.2, 7)^T / | w | · (8, 4)^T / | v |
    =   53.6/( | w || v |)

4. Assemble the projection:

   kv  =   | w | (w_u·v_u) v_u

   kv  =   | w |   [53.6 / (| w || v |)]   (8, 4)^T / | v |

   kv  =   53.6 / (| v |)   (8, 4)^T / | v |

   kv  =   53.6 / (| v |²)   (8, 4)^T

   kv  =   53.6 / 80   (8, 4)^T

   kv  =   ((53.6*8)/80, (53.6*4)/80)^T  =   ( 5.3, 2.68)^T

5. Compute the orthogonal vector:

   u  =   w - kv

   u  =   (3.2, 7)^T - (5.3, 2.68)^T  =   (-2.1, 4.32)^T