Answer:
Normalize each vector. This does not change the orientations. Now there are two unit vectors and the cosine of the angle between them can be found with the dot product.
Normalize each vector. This does not change the orientations. Now there are two unit vectors and the cosine of the angle between them can be found with the dot product.
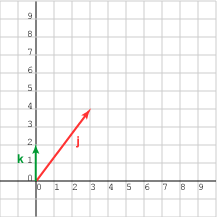
Find the angle between the two vectors:
j = (3, 4)T , k = (0, 2)T
First, find the length of each vector:
|j| = 5.0 , |k| = 2.0.
Normalize each vector. Often in this step it is wise not to perform the division:
ju = (3, 4)T / 5.0 , ku = (0, 2)T / 2.0
Compute the dot product:
ju · ku = (3, 4)T / 5.0 · (0, 2)T / 2.0 = (1/10)(3, 4)T · (0, 2)T = (0.1)(8) = 0.8.
Finally use the arc cos function of your calculator: arc cos 0.8 = 36.87°
Calculate the angle between: a = (10, 5)T and b = (8, 12)T