What is the cosine of the angle between the two unit vectors qu = (0.0, 1)T and wu = (-0.5, 0.866)T ?
Answer:
Again, cos x = 0.866. So it must be that x = arc cos 0.866 = 30°.
What is the cosine of the angle between the two unit vectors qu = (0.0, 1)T and wu = (-0.5, 0.866)T ?
Again, cos x = 0.866. So it must be that x = arc cos 0.866 = 30°.
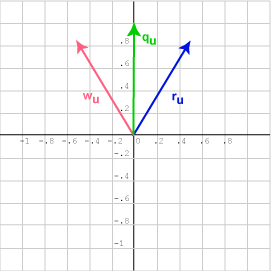
Both vectors ru and wu gave the answer cos 30, when the dot product was done with qu, although they lie on either side of qu.
In two dimensions, there are two unit vectors that are 30° away from a given vector. Both of them will give you the same dot product with the given vector. Be careful to draw a picture in ambiguous situations.
What is the cosine of the angle between the two unit vectors represented by qu = (0.0, 1)T and zu = (-0.5, -0.866)T ?