Orthogonality Detector and Length Calculator

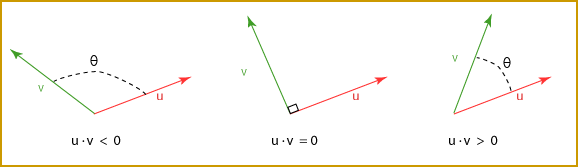
When two vectors are orthogonal (to each other) then their dot product is zero, regardless of their lengths. The dot product detects orthogonality no matter what the lengths of the vectors.

The sign of the dot product of two vectors u and v depends on whether the angle between them is acute or obtuse. If the value of the dot produce is zero, then the vectors are perpendicular.

Now look at the dot product of a vector with itself:

v · v  =  |v||v|cos 0° = |v||v| 1.0 = |v|2

The dot product of a vector with itself yields the square of its length.

|v| =  √(v · v)

Used in this fashion, the dot product calculates length. Since the two properties of a vector are length and orientation, you might suspect that the dot product is useful.