Watch those "-" Signs

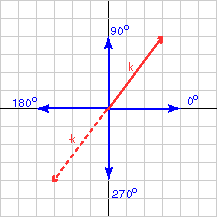
The diagram shows the vector represented by k = (3, 4)^T. Its orientation was calculated to be 53.13° to the positive x axis. That looks about right. The formula worked!

Now calculate the orientation of     -k = (-3, -4)^T.

Plugging into the formula:

arc tan( y/x ) = arc tan( -4/-3 ) = arc tan( 4/3 ) 
               = arc tan( 1.333333333333 ) 
               =  53.13°

Hmm... something is wrong. The formula gave us the same angle for a vector pointing in the opposite direction to the first. The problem is that information is lost when -4 is divided by -3. We can't tell the result from +4 divided by +3. The formula is not enough to give you the answer; you should sketch the vector and adjust the answer.

Look at the picture to see that the orientation of -k (expressed in degrees 0..360 counter clockwise from the x axis) is (180° + 53.13°) = 233.13°.