Answer:
The displacement from point B to point A is:
- The x displacement: 2-7 = -5
- The y displacement: 1-3 = -2
So the column matrix representing the displacement is:
e = (-5, -2)T
The displacement from point B to point A is:
So the column matrix representing the displacement is:
e = (-5, -2)T
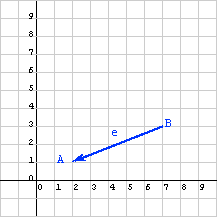
When the points are visited in the opposite order, the displacement vector points in the opposite direction. In the column matrix each element is -1 times the old value.
The displacement from A to B is different from the displacement from B to A. Think of displacement as "directions on how to walk from one point to another." So, if you are standing on point A and wish to get to point B, the displacement (5, 2)T says "walk 5 units in the positive X direction, then walk 2 unit in the positive Y direction."
Of course, to get from point B to point A you need different directions: the displacement (-5, -2)T says "walk 5 units in the negative X direction, then walk 2 unit in the negative Y direction," which puts you back on point A.
The displacement from point Start to point Finish :
displacement = (Finish x - Start x , Finish y - Start y)T
Say that point C is x=4, y=2 and that point D is x=3, y= 5 . What column matrix represents the displacement from C to D?
( )T