Picture of a Finite-State Automaton

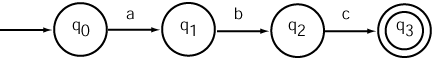
The diagram shows a finite-state automaton. This automaton recognizes the input string "abc" and no others. (The quote marks " " are not part of the string.)

An automaton consists of a finite number of states and transitions between states. In the diagram, the states are represented by the circles labeled q₀ through q₃. State transitions are represented by arrows between states and are labeled with zero or more characters.

The start state is the state that has an unlabeled transition leading into it. There is only one start state.

The final state is represented as two concentric circles. There can be one or more final states.

The "finite" in the term "finite-state automaton" means that there are only a finite number of states, not an infinite number of states. There are machines that are not finite-state. A machine that deals with analog values, an audio amplifier for example, has an infinite number of states. The signal is a continuous function of time, so it can assume an infinite number of values at each location in the machine. The "state" of such a machine at a particular instant in time is the exact value of the signal at each location in the machine. There are an infinite number of such states.