Regular Expressions

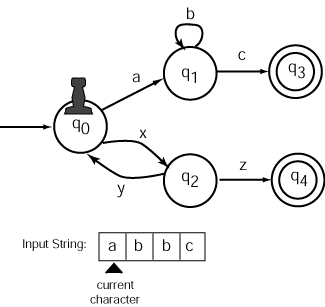
It is sometimes awkward to draw an automaton. A drawing takes up space and is not easily used as program input. A regular language can be described in a math-like manner using a regular expression. For example, the following regular expression describes the same language as the automaton at right.

(xy)*xz|(ab*c)

Don't worry (for now) about how the regular expression works. Regular expressions are discussed in another chapter.

A regular language can be described by either a finite automaton or by a regular expression. A laguage that can be described by one can also be be described by the other. To write a program that accepts a regular language it is easier to think in terms of a finite automaton.

Warning: in practice, the idea of regular expressions has been extended to include features that do not correspond to a finite automaton. The languages these extended regular expressions recognize are not always regular languages. Such an extended regular expressions is sometimes called a regex.

However, for the first sections of these notes a "regular expression" will correspond to a regular language, and both will correspond to a finite automaton.