created 05/22/2004
If you have read the chapters on
subroutine linkage,
write each exercise as a
main program calling a subroutine.
Use either the stack-based linkage or the
frame-based linkage convention.
Otherwise write the program as a single main.
In the Settings menu of SPIM set Bare Machine OFF, Accept Pseudo Instructions ON, Enable Branch Delays OFF, Enable Load Delays OFF, Enable Mapped IO OFF, Load Exception Handler ON.
Run the programs by clicking SimulatorGo and then OK in the pop-up panel.
Write a program that asks the user for x and then computes
exp(x) by using a Taylor series:
exp(x) = 1 + x + x2/2 + x3/3! + x4/4! + ...
exp(x) is ex, where e is the base of the natural
logarithms, 2.718281828...
You don't need to worry about the math behind this.
Just compute a sum of terms.
Each term in the sum looks like:
xn/n!
Designate a register to hold the current term. Initialize it to 1.0 (the zeroeth term). Term one is calculated by multiplying:
term*x/1
Term one is the value x. Term two is calculated by multiplying:
term*x/2
Term two is the value x2/2. Term three is calculated by multiplying:
term*x/3
Term three is the value x3/3!. Term four is calculated by multiplying:
term*x/4
... and so on. In general, after you have added term (n-1)to the sum, calculate term n by multiplying:
term *x/n
Keep doing this in a loop until the term becomes very small. Here are some example runs (with SPIM using single precision). As usual, only the first seven digits printed have any significance.
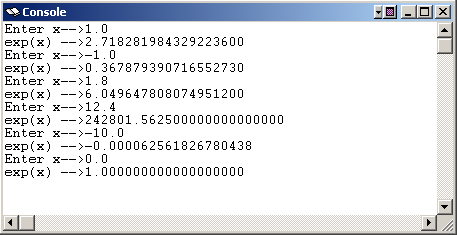
It might be helpful to first write this program in Java or C to verify your design, and then to proceed with the version in assembly language.
Click here to go back to the main menu.
Various infinite series for pi have been discovered. The first such series was
pi = 4( 1 - 1/3 + 1/5 - 1/7 + 1/9 - . . .)
This series is of little practical value because enormous numbers of terms are required to achieve good approximations (Acton, Calculus, 1999). However, it does provide good programming practice.
Write a SPIM program that writes out the sum of the first 1000, 2000, 3000, ... , 10000 terms of the series.
As with the previous program, write a version of this program in C or Java first to check that your design is correct.
Click here to go back to the main menu.
* == easy program ** == moderately easy program *** == harder program **** == project